Robot modeling and OCP formulation
Let us consider a torque-controlled planar robot with links of unit link lengths and masses. As represented in the figure below, the robot is contained in the XZ plane such that it is subjected to gravity.
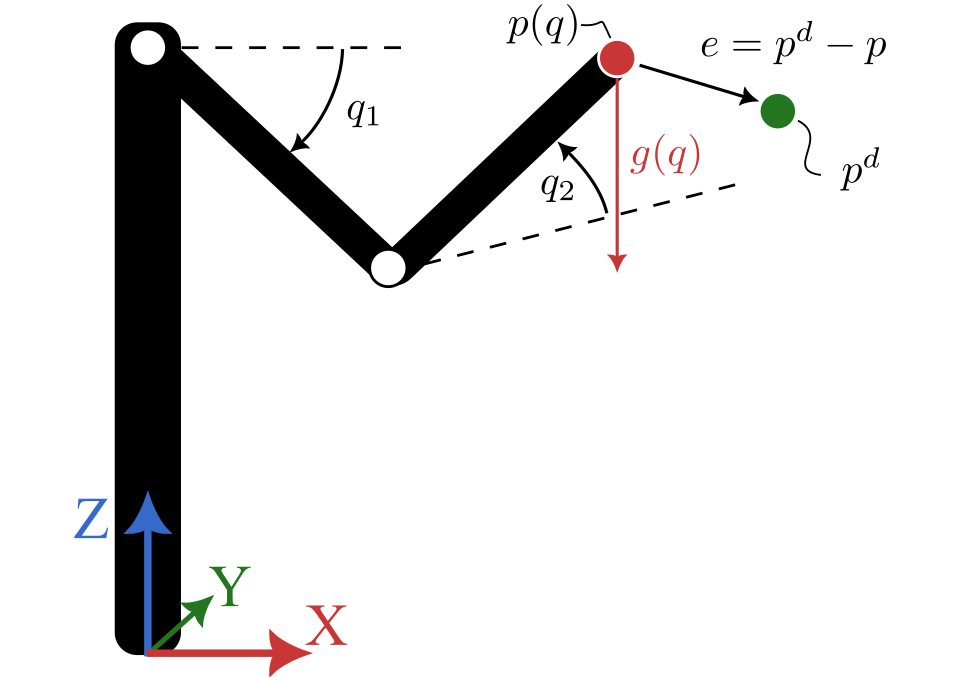
The goal of the controller is to compute control torques 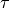 such that the robot tracks a desired Cartesian trajectory composed of a desired end-effector position
such that the robot tracks a desired Cartesian trajectory composed of a desired end-effector position 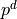 and velocity
and velocity 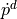 .
.
Robot dynamic modeling
The system can be described by the following dynamic model:

where
![q = [q_1, \, q_2]^T](../_images/math/d845aaa16ceea072ceab9f24df83b63a54ef82af.png) are the joint angles of the first and second links;
are the joint angles of the first and second links;![\tau = [\tau_1, \, \tau_2]^T](../_images/math/1fc1a9a5520602fcffedac2ea02997716f89c21f.png) are the torques applied to the first and second links;
are the torques applied to the first and second links;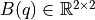 ,
, 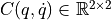 , and
, and 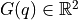 are the inertia matrix, the Coriolis matrix, and the gravity vector, respectively.
are the inertia matrix, the Coriolis matrix, and the gravity vector, respectively.
We can write the dynamic model in the form of a first-order differential equation with state ![x = [q, \dot{q}]^T](../_images/math/f9b6533cd8357a88113fdc6fd4b76f226b3de270.png) and control
and control  as follows:
as follows:
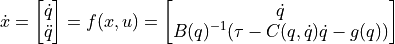
OCP formulation
In order to track the desired trajectory, the cost function 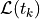 minimized by the predictive controller is defined at discrete time
minimized by the predictive controller is defined at discrete time 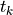 as
as
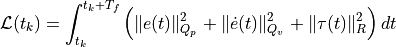
where  and
and 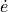 are the position and velocity tracking errors, respectively, and
are the position and velocity tracking errors, respectively, and 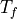 is the prediction horizon duration.
The weighting matrices
is the prediction horizon duration.
The weighting matrices 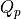 ,
, 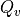 , and
, and 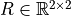 are positive definite matrices used to tune the closed-loop behavior of the robot.
are positive definite matrices used to tune the closed-loop behavior of the robot.
The control problem is subject to the following constraints:
the initial state
 is given;
is given;the joint positions are bounded by
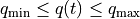 , with
, with ![q_{\min} = [-\pi, 0]^T](../_images/math/8117fbd9a2dc29c86e239e39cfdaf689b1cbb691.png) and
and ![q_{\max} = [-\cfrac{\pi}{2}, \cfrac{\pi}{2}]^T](../_images/math/864fbb4c98626e3f7e22095bd7d62a3ef6ad7f73.png) ;
;the joint velocities are bounded by
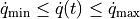 , with
, with ![\dot{q}_{\min} = [-2, -2]^T](../_images/math/b289d6889d9318970a347f88f75b203122b00b7d.png) and
and ![\dot{q}_{\max} = [2, 2]^T](../_images/math/120da319d76c94b25d815ded9ccbec061764e90c.png) ;
;the control torques are bounded by
 , with
, with ![\tau_{\min} = [-25, -10]^T](../_images/math/1f56ae79cc2b85b93aabe14181802ed8370e4eb5.png) and
and ![\tau_{\max} = [20, 10]^T](../_images/math/eb75e771cc6d67de3af54b0fb4a8a0bf7b87e689.png) .
.
Transcription using CasADI and Acados
The optimal control problem (OCP) is transcribed into a nonlinear program (NLP) using CasADi and Acados. The NLP is then solved by the Acados solver, which is a high-performance NMPC solver.
1) Define the CasADi symbols and parameters
The first step is to define the CasADi symbols and parameters of the robot model. Here, the geometry and mass properties of the robot are defined as model parameters.
import casadi as ca
# Define the CasADi symbols
sym_q = ca.SX.sym('q', 2) # joint angles
sym_q_dot = ca.SX.sym('q_dot', 2) # Joint velocity
sym_tau = ca.SX.sym('tau', 2) # Joint torques (controls)
# Define the CasADi model parameters
sym_l0 = ca.SX.sym('l0', 1) # position along Z axis of the joint [m]
sym_l1 = ca.SX.sym('l1', 1) # length of the first link [m]
sym_l2 = ca.SX.sym('l2', 1) # length of the second link [m]
sym_m1 = ca.SX.sym('m1', 1) # mass of the first link [Kg]
sym_m2 = ca.SX.sym('m2', 1) # mass of the second link [Kg]
2) Define the Acados model
The second step is to define the Acados model, which includes the state, controls, parameters, and dynamics. More details can be found in the Acados documentation.
from acados_template import AcadosModel
# Create an Acados model
model = AcadosModel()
model.name = 'rrbot'
# Define the state, control, and parameters variables
model.x = ca.vertcat(sym_q, sym_q_dot)
model.u = ca.vertcat(sym_tau)
model.z = ca.vertcat([]) # algebraic variables. N.B., actually used in the demo code
model.p = ca.vertcat(
sym_l0,
sym_l1,
sym_l2,
sym_m1,
sym_m2
)
sym_xdot = ca.SX.sym('x_dot', x.shape[0], 1)
model.xdot = sym_xdot
# Define the dynamics (not actually zeros...)
B = SX.zeros(2, 2) # Inertia matrix, function of q, l1, l2, m1, m2
C = SX.zeros(2, 2) # Coriolis matrix, function of q, q_dot, l1, l2, m1, m2
G = SX.zeros(2, 2) # Gravity vector, function of q, l1, l2, m1, m2
expr_q_dot2 = ca.inv(B) @ (sym_tau - C @ sym_q_dot - G)
# Explicit ODE model
model.f_expl_expr = ca.vertcat(
self.sym_q_dot,
expr_q_dot2 # joint acc. from torques
)
# Implicit DAE model
model.f_impl_expr = ca.vertcat(xdot - model.f_expl_expr)
# Forward kinematics
# - Cartesian position of the end-effector
sym_p = ca.vertcat(
sym_l0 + sym_l1 * ca.sin(sym_q[0]) + sym_l2 * ca.sin(sym_q[0] + sym_q[1]),
sym_l1 * ca.cos(sym_q[0]) + sym_l2 * ca.cos(sym_q[0] + sym_q[1])
)
# - Cartesian velocity of the end-effector
sym_p_dot = ca.jacobian(sym_p, sym_q) @ sym_q_dot
The full code can be found in the rrbot_model.py file in the example_acados_controller/script directory of the acados_solver_ros2_examples repository.
3) Define the Acados OCP
The third step is to define the Acados optimal control problem (OCP) by specifying the cost function, constraints, and solver settings. It should be noted that we use a nonlinear cost function, but a linear cost could easily be used instead.
from acados_template import AcadosOcp
import numpy as np
N = 10 # default prediction horizon length (num of sampling periods)
Ts = 0.1 # sampling time
# Create an Acados OCP
ocp = AcadosOcp()
ocp.model = model
# Declare extra parameters to use in the cost function
sym_p_ref = ca.SX.sym('p_ref', 2)
sym_p_dot_ref = ca.SX.sym('p_dot_ref', 2)
sym_Q_pos_diag = ca.SX.sym('Q_pos_diag', 2)
sym_Q_vel_diag = ca.SX.sym('Q_vel_diag', 2)
sym_R_diag = ca.SX.sym('R_diag', 2)
# Append extra parameters to the model parameters
model.p = ca.vertcat(
model.p, # original model parameters (see rrbot_model.py)
sym_p_ref, # reference position
sym_p_dot_ref, # reference velocity
sym_Q_pos_diag, # weight for position error
sym_Q_vel_diag, # weight for velocity error
sym_R_diag, # weight for control (torques)
)
# set default parameter values
ocp.parameter_values = np.zeros((model.p.shape[0],))
# Define the (non-linear) cost function
Q_pos = ca.diag(sym_Q_pos_diag)
Q_vel = ca.diag(sym_Q_vel_diag)
R = ca.diag(sym_R_diag)
err_p = sym_p_ref - sym_p
err_p_dot = sym_p_dot_ref - sym_p_dot
ocp.cost.cost_type = 'EXTERNAL'
ocp.cost.cost_type_e = 'EXTERNAL'
ocp.model.cost_expr_ext_cost = \
err_p.T @ Q_err_p @ err_p \
+ err_p_dot.T @ Q_err_p_dot @ err_p_dot \
+ rrbot_model.sym_tau.T @ R @ rrbot_model.sym_tau
# Note: the terminal cost should be chosen more carefully in practice.
# This is not very rigorous, but enough for the purpose of this example.
ocp.model.cost_expr_ext_cost_e = \
err_p.T @ Q_err_p @ err_p \
+ err_p_dot.T @ Q_err_p_dot @ err_p_dot
# Define the constraints
# - placeholder for initial state
ocp.constraints.x0 = np.zeros((model.x.shape[0],))
# - joint torque limits
ocp.constraints.idxbu = np.array([0, 1])
ocp.constraints.lbu = np.array([- 25., - 10.])
ocp.constraints.ubu = np.array([25, 10])
# - joint position and velocity limits
q_dot_max = 2
ocp.constraints.idxbx = np.array(range(model.x.shape[0]))
ocp.constraints.lbx = np.array(
[- np.pi, - np.pi / 2., -q_dot_max, -q_dot_max])
ocp.constraints.ubx = np.array(
[0., np.pi / 2., +q_dot_max, +q_dot_max])
# - terminal (state) constraints
# (we simply replicate stage state constraints)
ocp.constraints.lbx_e = ocp.constraints.lbx
ocp.constraints.ubx_e = ocp.constraints.ubx
ocp.constraints.idxbx_e = ocp.constraints.idxbx
# Set solver options
ocp.solver_options.N_horizon = N # number of shooting nodes
ocp.solver_options.tf = N * Ts # prediction horizon in seconds
ocp.solver_options.nlp_solver_type = 'SQP_RTI'
ocp.solver_options.integrator_type = 'IRK' # use implicit DAE model
... # other solver options (see the full code or Acados documentation details)
All done, at this point, the OCP is fully defined and can be used in Python applications (see AcadosOcpSolver).
The full code can be found in the export_acados_solver_plugin.py file in the example_acados_controller/script directory of the acados_solver_ros2_examples repository.
Notes
The cost function is implepmeneted as a
EXTERNALnon-linear function, but theNONLINEAR_LScost function could be used instead for better performance.- This is an example application, but in practice additional features could be implemented, such as:
considering a more rigorous terminal cost function (e.g., LQR-like) and constraints (e.g., terminal set);
adding some slack to state constraints;
using the derivative of the torque as control variable (instead of the torque itself) so as to limit jerk.